Quadratic equation paradox
$x^2+x+1=0$
Let's rewrite our equation in two equivalent forms:
$1)\quad x\cdot(x+1)=-1$
$2)\quad x+1=-x^2$
We get:
$x\cdot(-x^2)=-1$
$x^3=1$
$x=1$
Triangle paradox

|
Consider an arbitrary triangle $ABC$.
Let $m$ be a perpendicular bisector of $AC$ (divides $AC$ on two equal intervals)
and $l$ - angle bisector (divides $B$ on two equal angles), $O$ - intersection of $m$ and $l$. Now we can see that $\alpha_1=\alpha_2$ and $l_1=l_2$ (because $m$ is a perpendicular bisector). $h_1=h_2$ (because $l$ is an angle bisector). We see that the right-angled triangle with the hipotenuse $l_1$ and the cathetus $h_1$ is equal to the right-angled triangle with the hipotenuse $l_2$ and the cathetus $h_2$ (because $h_1=h_2$ and $l_1=l_2$). This means that $\beta_1=\beta_2$. So we come tho the result that $A=C$ (because $\alpha_1=\alpha_2$ and $\beta_1=\beta_2$). Analogically we can prove that $A=B$. Finally we proved that any triangle $ABC$ is equilateral: $A=B=C=60^{\circ}$ 
|
Derivation paradox
Consider any smooth vector function $\overrightarrow{r(t)}$ s.t. the vector and it's derivation are never equal to zero. We denote vector's length as $r=|\overrightarrow{r}|$
$r^2=\overrightarrow{r}\cdot\overrightarrow{r}$
$2r\cdot\dot{r}=2\overrightarrow{r}\cdot\dot{\overrightarrow{r}}$
$2|\overrightarrow{r}|\cdot \dot{|\overrightarrow{r}|}=2|\overrightarrow{r}|\cdot{|\dot{\overrightarrow{r}}|}\cdot \cos(\angle\overrightarrow{r}\dot{\overrightarrow{r}})$
We see that cosinus of the angle between $\overrightarrow{r}$ and it's derivation $\dot{\overrightarrow{r}}$ is equal to 1.
So at any time $t$ vector $\overrightarrow{r}$ is parallel with it's derivation $\dot{\overrightarrow{r}}$. Nonsense! Where is the mistake?
Ellipse paradox
Consider any ellipse
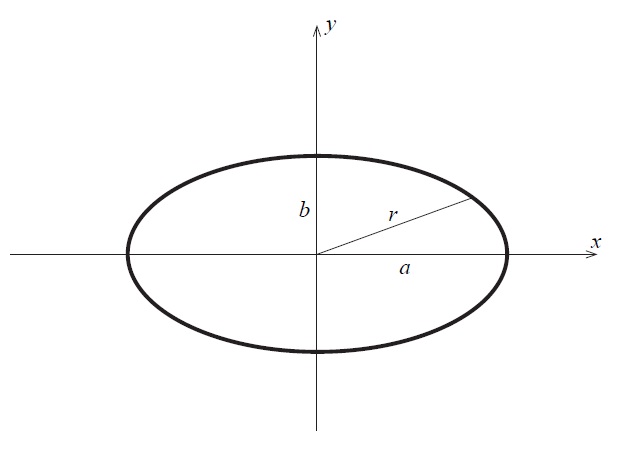
$x=a\cos\varphi,\quad y=b\sin\varphi$
We know that the area of ellipse is $S=\pi ab$. Let's try to derive the formula for this area:
$\displaystyle\pi ab=S=\int\limits_0^{2\pi}\frac12r^2d\varphi=\int\limits_0^{2\pi}\frac12(x^2+y^2)d\varphi$
$\displaystyle=\int\limits_0^{2\pi}\frac12(a^2\cos^2\varphi+b^2\sin^2\varphi)d\varphi=\frac{\pi}{2}(a^2+b^2)$
So we see that $\displaystyle ab=\frac{a^2+b^2}{2}$
It means that $a=b$, i.e any ellipse is a circle.